Food Shortages And Speculation Is The Next Offensive Against The Population!

Background 

World population is projected to reach 9–11 billion by 2050, raising concerns about food system security and sustainability. Modeling food systems are often a way to understand current and future dynamics. The most common model, first articulated by Malthus (Malthusian), shows population growth as an exponential function and food production as a linear function, concluding that human carrying capacity will be reached leading to mass starvation. Another prominent model was introduced by Boserup (Boserupian), which explains increases in food production as a function of population growth.

Methodology 

Here, we explore which food systems dynamics exist at equilibrium and after perturbation. The model introduced explores food availability in an isolated village and then in a line of villages. The isolated village model includes three key parameters: maximum calorie production (a), food production resilience (b), and minimum calorie requirement per person (c). The multiple village model adds an additional parameter for trade.

Results 

Isolated village populations are more resilient to famine than Malthusian theory predicts, suggesting that Malthus’ premise may be inaccurate. Predictably, across multiple villages increasing access and production reduce famine. However, under certain conditions large amounts of transport can lead to antagonist relationships leading to rapid changes in population.

Conclusion 

Food systems under both production and access scenarios proved to be resilient to small perturbations, requiring a large catastrophe to induce mortality; this appeared to discount the Malthusian model. This model can create dynamics where different modes of famine relief apply, but here we see that a balanced approach of both access and production appears to be the most resilient to famine.

Background

Understanding the limitations of food systems that support human population growth has profound implications for natural resource management and agricultural productivity. Food security means the availability of sufficient food at all times for all people in order to ensure an active and healthy life, which is a challenge to humanity. It is broadly accepted that food security is a human right (Universal Declaration of Human rights article 25), yet food security is still a major problem worldwide. Food security is maintained when food systems are resilient (responsive to perturbations) to increases in population in addition to instability in production caused by natural disasters (e.g., floods, droughts), political strife, disruptions to transportation/distribution networks, lack of storage capacity, economic stress, and increasingly climate change. These challenges can work individually or interact, which may facilitate new interactions that may create new famines with different intensities.

Despite the consensus that famine is caused by complex local interactions, it is often simplified into Neo-Malthusian paradigm; or the Boserupian paradigm. The Malthusian paradigm is based on understanding human carrying capacity of environments. Therefore, once the population has exceeded the food production, catastrophic famine will ensue. The Boseruprian model looks at increasing population as a catalyst for agricultural intensification leading to increased productivity, however this perspective is less dominant in agricultural circles. A major debate in development has been on the best way to create food security, either neoliberal forms of governance (e.g., market integration) or food sovereignty approaches (e.g., agroecological/low-input mixed land use high human labor). Neo-Malthusian doctrine gains popularity every generation; it was most famously discussed in the 1960s and 1970s. These solutions are often more simply stated as: an ‘access’ paradigm; or a ‘production’ paradigm. The access paradigm suggests that we simply lack the appropriate infrastructure and political will to provide adequate food. The production paradigm suggests that we lack the technological capacity to produce enough food for everyone or that this technology has not diffused to those who need it. The access and production viewpoints have often been seen as antagonistic toward each other, with proponents of the different paradigms offering drastically different development strategies to alleviate famine. These viewpoints necessarily oversimplify the issue, allowing for an obfuscation of local dynamics, but make policy recommendations easier. These local dynamics include the social structure of communities that can have dramatic impacts on the amount of cooperation or antagonism within a community during a famine. This implies that there is wide parameter space when communities experience famine, both for recovery and for catastrophic failure.

Fig. 1

Recently, Neo-Malthusian doctrine has become common with worldwide population projected to increase  9–11 billion by 2050 and subsequent concerns about food security. In an effort to understand the cyclical interest in Malthusian doctrine, there has been an effort to understand stresses to historic agriculture systems and retrospectively understand the causes of specific famine events. The definition of famine has continuously evolved and includes mortality due to war, starvation, malnutrition, and disease under food stress. Defining famine continues to be a challenge as more information is available for human systems including: nutrition information; hungry season vs. crop failure; poverty; political instability; disease related to malnutrition; migration-related disasters; trade imbalances; natural disasters ; food hording ; and social stratification. Issues of attribution of the factors that cause lethal famine, are still up for debate, due to all starvation rarely being the cause of death reported on death certificates. Here, we aim to understand the dynamics of famine in a single location as well the dynamics of how famine events propagate through space and time through a simple mathematical model. This model is used to compare different paradigms of famine and famine recovery through simulation with simulation results being compared to historic famine events to assess reliability.

Materials and methods

Baseline village that is isolated and not in contact with other villages

Conceptualization of model

We approach this problem using a discrete model where the time steps can naturally be defined as harvest seasons. The model includes two variables: Pn and En. Pn represents the working human population at the nthℎ season while En represents the calories of excess food available at nthℎ season. Because the village is isolated, all of the food is locally produced and there is neither immigration to the village nor emigration from the village; hence any fluctuations in human population is exclusively due to death. We restrict our study to short periods of time, 0–5 years to see the immediate effects of famine upon a population. With this restriction, the new births will not provide meaningful impact on the food production as the children have not matured to a working age. Additionally, after natural disasters there is frequently increased fertility after the disaster that helps population recover.

The village can be thought of as a subsistence village, which can be broadly defined as agriculture where the majority of the output is consumed by the village rather than marketed for profit. In our first simulations, we assume the village is isolated, implying that there is no importing or exporting of food. Thus, all the food grown locally is the only food available for consumption. When we later consider multiple villages, we will relax this assumption and allow for importing and exporting of food between neighboring villages. Within this village there is no formal social structure, the model looks at the number of people needed to produce and maintain a population, rather than how those calories are distributed. In essence, this can be conceptualized as a village with a single social class, the working class.

The model also makes the assumption that production technology remains stable, i.e., advances in food production are negligible over the duration of the simulation. Though a technological breakthrough may improve quality of life for the villagers especially during a famine, the investment of labor and capital for a technological advancement may not be feasible for the current economical model of a village; it is simply easier to keep the current production technology and or methods. This phenomenon is what Boserup referred to as “technical inertia”. It is also plausible that a production system can become so specialized that it cannot adapt in response to such drastic perturbations as evidenced by the Rust Belt in the 1970s.

In each modeled village we consider a fixed, finite amount of land available for production. Using Malthus’ theory of diminishing marginal product, this will imply that the production system will eventually reach a plateau despite increasing input resources such as workers or seeds.

Determination of the excess of food available in the next season

We define the excess food to be the calories available after the individuals of a population have consumed their minimal calories needed per season. Therefore, excess food is the total calories produced minus the calories consumed. Assuming each individual consumes an average of c calories per season, we can say the total consumption by the entire population Pn at the nthℎ season is cPn.

The number of calories produced in a season depends on factors such as the number of workers available, the supply of seeds, and agricultural land availability. According to the economic concept of diminishing marginal product (DMP), the production function should eventually plateau, or approach a maximum, as one of these resources increases with the other resources fixed. In this model, the total amount of food produced is represented by a product of the availability of the workers and the supply of seeds available in a fixed area of land.

For the calories of food due to workers, we consider the function, p(Pn)=aPn1+bPn()=1, which increases monotonically from 0 and exhibits the desired plateau behavior as the number of people increases. The value ab represents the maximum production capacity of calories by the people and 1b1 represents the characteristic number of workers needed to saturate the production function.

To factor the supply of seeds into our production function, we desire a function that increases production as more seeds are available up to a certain maximum to satisfy the concept of DMP. Additionally, the function should always have a supply of seeds available as during times of shortage people are reluctant to use their entire supply of seeds. Assuming that seeds are proportional to the excess food supply, we propose the function s(En)=(1+tanh(fEn))()=(1+tanh⁡()) to satisfy both of these conditions, where f is a positive constant that models how resilient the systems is to fluctuations in food supply. Greater values of f correspond to a more sensitive system while lesser values of f correspond to a highly resilient system. This functional form satisfies the DMP condition because it increases monotonically as seeds are more available (or as En increases) until an upperbound of 2, and a supply of seeds is always available as it approaches but never equals 0 during a food shortage (or as En becomes more negative).

By multiplying p(Pn)() and s(En)(), we obtain the total calorie production in the next season, aPn1+bPn(1+tanh(fEn))1+(1+tanh⁡()) By subtracting the calories consumed in the previous season, we obtain the excess calories available in the next season: En+1=aPn1+bPn(1+tanh(fEn))−cPn+1=1+(1+tanh⁡())− (Table 1).Table 1 Model parameters and the interpretation of their values. Parameters are constants with modifiable values that characterize a specific region’s food production

Determination of the human population in the next season

We assume the human population will not change if there is an excess of food (En>0>0) and will decrease if there is a shortage of food (En<0<0). Assuming the number of deaths is proportional to the shortage of food at a rate of d>0>0 deaths per calorie deficiency, we have

Pn+1={PnPn+dEnEn>0,En≤0.+1={>0,+≤0.

(1)

In summary, the model consists of the following system of difference equations:

Pn+1En+1={PnPn+dEnEn≥0,En<0,=aPn1+bPn(1+tanh(fEn))−cPn.+1={≥0,+<0,+1=1+(1+tanh⁡())−.

(2)

Non-dimensionalization of model

In order to ease the analysis of the model, we reduce the number of parameters by non-dimensionalizing the model equations. We introduce non-dimensional variables Pn¯¯¯¯¯¯=bP¯= and En¯¯¯¯¯¯=bdEn¯= and let a¯¯¯=ad¯=, b¯¯=fbd¯=, and c¯¯=cd¯=. After all of these substitutions, we have the following non-dimensional model:

Pn+1¯¯¯¯¯¯¯¯¯¯En+1¯¯¯¯¯¯¯¯¯¯¯={Pn¯¯¯¯¯¯Pn¯¯¯¯¯¯+En¯¯¯¯¯¯En¯¯¯¯¯¯≥0,En¯¯¯¯¯¯<0,=a¯¯¯Pn¯¯¯¯¯¯1+Pn¯¯¯¯¯¯(1+tanh(b¯¯En¯¯¯¯¯¯))−c¯¯Pn¯¯¯¯¯¯.+1¯={¯¯≥0,¯+¯¯<0,+1¯=¯¯1+¯(1+tanh⁡(¯¯))−¯¯.

(3)

For the rest of this paper, we will drop the bar notation and the reader may assume that any reference to the model variables and its parameters are the non-dimensional variables and parameters as listed in Table 2. The non-dimensional parameter a can be interpreted as the ratio between the amount of calories produced by each person and the deficiency in calories leading to the death of a person. The non-dimensional parameter b is the typical surplus or shortage of food in the model, measured in terms of the food changes needed to induce significant increases or decreases in the saved seeds. It can be interpreted as a measure of sensitivity: low values of b mean that changes in food supply have minimal effect on the food production, which would be governed predominantly by the number of people in that case. If the value of b is high, it means that food production is governed not only by the number of people, but also by any food surplus or shortage in the past. The non-dimensional parameter c is similar to a, except that c is a measure of consumption instead of production by each person. The advantage of presenting non-dimensional population is that any subsequent changes can be interpreted as a proportion of the initial population, regardless of the specific numbers that may differ depending on the particular application of interest.Table 2 Model parameters with dimensions removed and their interpretation on how they affect the model

Equilibria of model

Equilibria are tuples, (P∗,E∗)(∗,∗), where neither P∗∗ nor E∗∗ change from one season to the next. The trivial solution for P∗∗ and E∗∗ is when there are neither people nor food, (0, 0). Non-trivial solutions solve the following equation:

E∗=aP∗1+P∗(1+tanh(bE∗))−cP∗.∗=∗1+∗(1+tanh⁡(∗))−∗.

(4)

Observe that the values of a, b, and c affect the equilibrium values of the equation. Given set values for a, b, and c, one can use standard root-finding schemes to numerically solve for the non-trivial solutions (P∗,E∗)(∗,∗).

After finding the equilibrium for a given set of parameters a, b, and c, we simulate the model using initial values (P0,E0)(0,0) chosen from evenly spaced grid of points. We then record which points return to a non-trivial equilibrium and which return to the trivial equilibrium.

When famine strikes a village it can either trade or attack a neighboring village to reach a stable amount of food for its population

Justification for trade parameters

To study the effect of food transport between neighboring villages, we extend the isolated village model to incorporate a line of equally spaced villages. The food produced and the human population at each village are assumed to evolve in the same way as in the isolated model, except that we now allow food (but not humans) to move between adjacent villages. The only modification we need is in the expression for the excess food given in Eq. 2, where we add or subtract any transported food accordingly. Here, we consider a second-order central-difference scheme of a simple diffusive process, such that the excess food before trade Ei at the ithℎ village is adjusted by the net gain/loss of calories from/to its neighboring villages:

k[Ei−1−2Ei+Ei+1],[−1−2++1],

(5)

where k is a positive parameter measuring the rate of food transfer between adjacent villages. A large or small k, respectively, represents an infrastructure supporting efficient or poor trade. The model allows a village having more/less excess food than its adjacent villages to lose/gain through trade.

Now the excess food produced locally by the food system, Ei,,, and the human population, Pi,n,, at the ithℎ village will rely on the food after transfer Eneti,n, at the nthℎ time step.

Updating Eq. to reflect these changes produces:

Eneti,n+1Ei,n+1Pi,n+1=Ei,n+k[Ei−1,n−2Ei,n+Ei+1,n],=aPi,n1+Pi,n(1+tanh(bEneti,n))−cPi,n,={Pi,nPi,n+Ei,nEneti,n>0,Eneti,n<0,,+1=,+[−1,−2,++1,],,+1=,1+,(1+tanh⁡(,))−,,,+1={,>0,,+,,<0,

(6)

To predict the global and long-term effect of a sudden and local famine event, we conducted a series of simulations as follows. Before famine strikes, the villages are assumed to have the same excess food and population values, which are obtained from equilibria in the isolated model. At the first time step, we introduce a decline in excess food at one village located at the origin. By reflective symmetry at the origin, all villages to the left are expected to behave in the same way as the villages to the right, so we only monitor the villages to one side. The resultant changes in excess food and human population along the line of villages were simulated over time. We terminated the simulation either when a village population went extinct or when a village sufficiently far away experienced the effect of famine at the origin.

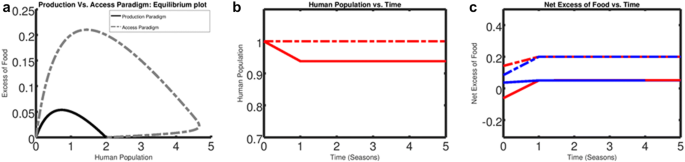
Using the multiple village model, we simulate two competing paradigms for preventing famine, the production and access paradigm (see introduction). In each paradigm, the villages are all assumed to have the same initial population. To characterize the production paradigm, each individual has more resilient food production systems (lower b parameter), but inefficient food transportation infrastructure (lower k parameter). In contrast, villages in the access paradigm have unstable food production systems, but efficient food transportation to alleviate these individual deficiencies.

Results and discussion

Individual subsistence village with stable farming technology

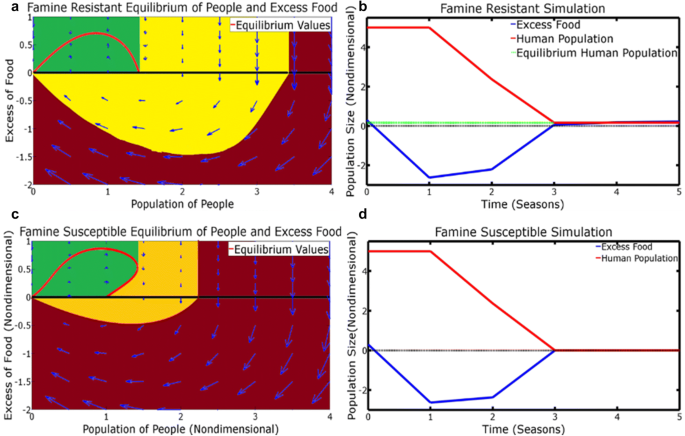
We are exploring a specifically defined subsistence village with three parameters used to explore famine in an isolated village: maximum production of food (a), food production resilience due to seeds (b), and minimum calorie requirement per person (c). There are two qualitatively different cases depending on the three parameters: if b(a−c)≤1(−)≤1, then the village is famine resistant (Fig. 2a), however if b(a−c)>1(−)>1 then the village is famine susceptible (Fig. 2c). In the famine-resistant case, there was a large set of initial conditions where an isolated village was resilient to famine, implying that, while famine could continue for multiple seasons, populations could recover back to a stable state thus regaining equilibrium (Fig. 2a, c). This large set of initial conditions (shaded in yellow), where recovery from famine is possible, suggests that the system needs to be dramatically perturbed to cause famine. It is important to note that this simulation only takes into account death from starvation. Though famine makes people more susceptible to disease, much of the literature suggests that mortality may not directly result from lack of calories.

Fig. 2

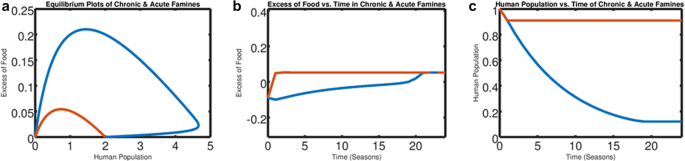
It is possible to identify famines that are quickly resolved and those that persist through time by adjusting the value of the food production resilience due to seed supply, b and keeping all other parameter values constant, drastic differences in the response of the village due to famine were observed (Fig. 3). In this scenario, greater values of b correspond to lesser food production resilience and lower values of b correspond to a greater food production resilience. Though a higher value of b accommodates equilibria for larger population sizes and larger food production, we observe the village suffers both a greater loss of human life and longer recovery period when hit with a famine event at these higher values of b. Due to the contrast in duration of the famines, we classify the famine as chronic for the higher value of b and acute for the lower value of b.

Fig. 3

Multiple villages

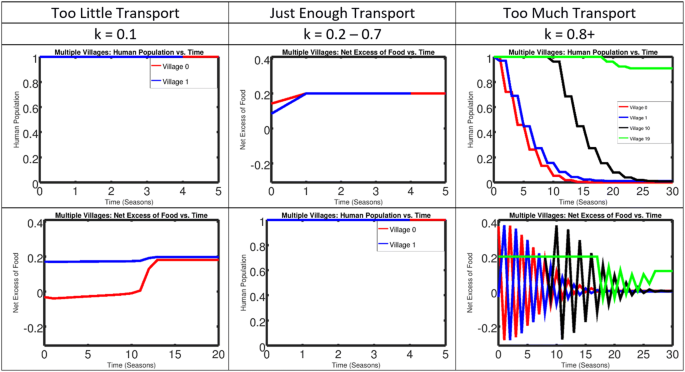
A multiple village model was created by simulating different amounts of food transported between villages using the k parameter, with all other parameter values fixed (Fig. 4). Qualitatively there are three different outcomes. When there is insufficient transport between villages, the multiple village model behaves similarly to the isolated village model. We observe that the famine is spatially constrained to the center village (Village0Village0) affected as the population of adjacent villages’ (Village1Village1) remain in equilibrium. Even with relatively little transport between villages, the benefits of trade greatly improve the survival of Village0Village0. Compared to the isolated village model (Fig. 3), Village0Village0 retains 60%60% more of the initial population and recovers from famine about five seasons quicker. When there is a sufficient transportation of food between villages, famine is averted completely, due to the aid of adjacent villages, Village0Village0 recovers from famine within one season, avoiding any deaths due to starvation. However, when there is too much transportation between villages we observe a seemingly antagonistic scenario, where villages are in desperate need of food, alternating between states of surplus and shortage. In this scenario, the famine spreads catastrophically through space decimating villages in its wake over the course 30 seasons. This is qualitatively similar to patterns observed in long-term conflicts and places where aid has been ineffective. We also observe that famines progress over time in different ways under the ‘production’ and ‘access’ paradigms (Fig. 5). Both methods are able to alleviate famine, however the access seems to provide greater resiliency yet have less stability, presenting multiple options when identifying potential solutions (Fig. 5).

Fig. 4

Fig. 5

Population dynamics: isolated village

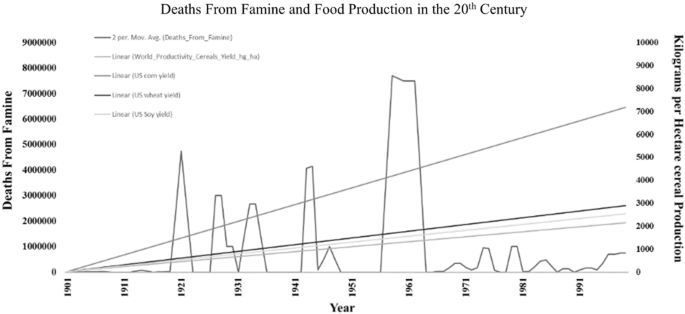
Individual villages were resilient to famine, it was difficult to induce famines that caused large mortality or extinction of the population. This is consistent with the thought that complex interactions drive famine rather than single factors such as production. This is exemplified by the lack of relationship between production and death from famine in major famines of the twentieth century (Fig. 6). The expectation under both Neo-Malthusian doctrine and the ‘production’ paradigm is that a small isolated village should be very susceptible to famine, however, our results suggest that in a simple model of production an isolated village is more resilient than expected. This resiliency has impacts based on how to evaluate famine, and what interventions would be most appropriate. A limitation of this model is that it assumes isolated populations all participate in the subsistence economy; the limited economy provides a simplified version of a society but does capture the qualitative dynamics of a famine. Here we find that the small villages might be more resilient than expected from a simple Malthusian model and may in fact have dynamics more similar the Boserupian model. A limitation of the isolated model is the reliance on the subsistence economy creates a more closed system that would be expected in reality, but the dynamics of recovery provide insight into the real world.

Fig. 6

Population dynamics: multiple villages

To explore if increasing the size of a food network improved resilience, a group of villages laid out in a line was explored for resiliency. The model was set up such that a comparison could be made between the ‘production’ paradigm and the ‘access’ paradigm. While it is known that many factors influence trade, this model simply explores the magnitude of this effect. Those who favor the access paradigm point out that food transport is relatively straightforward, food aid has been a useful mechanism to alleviate famine, and that land tenure systems can be maintained if more land does not need to be brought into production. However, food systems contain points of vulnerability which influence food availability and nutritional quality such as; black markets, food waste, distance between people and markets. When trade is conducted a large range of distances are relevant as food travels  1500–3700 miles from production to market on average, but there are high value local markets where food travels less than 50 miles. The distance food travels to market which can account for 50%50% of costs associated with getting food to market. The distance food travels is important because as food travels intermediaries between producers and consumers can increase the price of food for consumers, increasing starvation in times of food insecurity. This model does not directly test for antagonistic interactions between villages, it assumes that if excess food is present it will be traded. This assumption limits the ability to test interactions that cause food insecurity due to political instability. In our model, we address famine amelioration through trade, assuming that if food is available in an adjacent village, trade will occur. This implies that multiple villages along the line both need to experience crop failure, for famine to cascade through space, as purchase is not explored we cannot determine if adding complexity to the economy would cause individual villages to go extinct at the expense of some villages surviving.

Cyclical nature of famine and the response of famine over time

Famine is both biological and a social phenomenon; this complex interaction causes many different responses. People who are vulnerable to famine create defined responses to minimize this vulnerability over time. Additionally, famines generally influences the young and the old, this may also have led to religious connection to fasting, which decreases the food intake of healthy individuals for a substantial portion of the year (e.g., Orthodox Christians and Orthodox Jews). When famines are acute, responses are frequently instantaneous in the form of disaster relief or migration, however if famine persists into a more chronic state then grassroots efforts at a smaller scale must fill in this food gap. Most prediction mechanisms are based on the idea of dealing with an acute disaster aid and is not focused on chronic malnutrition.

Famine impacts social groups differently in society changing famine dynamics. Long-term population cycles until the modern era seem to fit this cyclical dynamics, while there are many causes, famine certainly is one. Famine can be cyclical, for example, observed a strong correlation between war-peace cycles and population levels in response to climate. This implies under climate stress that there would be a strong seasonal variation in famine and food production. Famine is often described as complex interaction between markets, production, social norms, and the environment. Cyclical famines can be continued when simplistic explanations are used to develop policy solutions to famine, for example focusing on a technical solution without addressing social solutions. Conflict combined with periodic food shortages can lead to famine, especially when it is combined with a relatively inflexible agriculture sector (such as our model), leads to cyclical famine.

Historic examples of response to famine

Different parameter sets within the multi-village model identified scenarios where proximate villages behaved in both cooperative and competitive ways. This shows that there are multiple pathways to food security and that local dynamics will likely dictate which path is the best to pursue, and that there are qualitative similarities to historical famines can be represented by simple parameter sets (Table 3). One such example is the Norse settlements in Greenland where the Vikings had steady decline rather than abrupt extinction where the critical parameter was k (trade), as there was limited land for production due to the glaciated landscape. The changing amount of trade combined with inter-annual climate variation caused periodic famine leading to a long and steady decline, with intermittent increases in population due to migration. After large-scale trade stopped at the end of the 1300s, there were increasingly antagonistic relationships with the Thule Inuit, therefore the combination of decreased agricultural capacity, decreased trade, and increasing conflict led to a decline and extinction of the settlements. In other historic famines the critical parameter is different, for example in Somalia in 2012 the critical parameter was b (sensitivity to perturbation). In the 2012 famine there was a complex combination of factors that included inadequate production and limited access to aid that limited adaptive capacity. Long-standing structural problems due to the ongoing civil war that exacerbated a production shortfall, this was coupled with very high global grain prices, this caused a famine as there was limited adaptive capacity due to the confluence of events. However, the population quickly recovered, showing a surprising amount of resiliency even in an unstable situation. The resilience in this case was in population growth to drops in food production and the ability of food aid to ameliorate food production decreases. A final historic example is the great leap forward in China where there were over 30 million deaths, this is an example of the critical parameter being a (food production). Here population relocation and industrialization led to a decrease in agricultural production capacity. This lack of production and loss of farming expertise led to a widespread famine. This shows that while there are complex issues surrounding famine, they can be represented in a fairly simple manner, and that this model does not appear to match the catastrophic prediction of Malthusian dynamics.Table 3 Famine can occur for many reasons. Here, we explore the causes of historical famines and how they can be interpreted using the model parameters a, b, and k

From the simple to the complex: relating to the real world

Food production has steadily increased over the course of the twentieth century. Despite these increases, recent studies have expressed the idea that food production needs to nearly double by 2050 to keep pace with population. There is acknowledgement that famine is both spatially and temporally complex and that it is due to interactions. Most recent assessments of famine recognize that it is a complex situation that has to do with (1) food production; (2) food access and purchasing power; (3) sanitary conditions for preservation and utilization; (4) natural environment, and (5) political constraints. In general, the model constructed here shows that even under strong perturbation societies can rapidly reach new equilibria and maintain themselves. The multiple village model showed that famine could be ameliorated with either production or trade. This scenario also showed that famine did not propagate very far in space or time and that the system became more stable as more villages were added to the system. This favors the Boserupian model over than Malthusian model, which suggests that population collapse should occur.

Conclusions

Exploring through simulation how famine occurs in both individual villages and groups of villages is a powerful tool for understanding the qualitative dynamics of human population capacity. Food systems under both production and access scenarios proved to be resilient to small perturbations, requiring a large catastrophe to induce mortality. This appeared to discount the Malthusian model. Famines propagated in space, but tended to be temporally restricted, not spreading through different time steps (seasons of food production). This model can create dynamics where different modes of famine relief apply, but here we see that a balanced approach of both access and production appears to be the most resilient to famine. These simulations provide insight into the way the food system can be monitored. Understanding the best way to monitor food security is a major goal of the international community. Different metrics have been proposed, and subsequently revised. The metrics have been focused both on calorie production and nutritional value of those calories, often focusing on the economic conditions and public health indicators within households. Different disciplines focus on the different facets of food security focusing on the disciplinary emphasis (e.g., production, purchasing power, child malnutrition). Further, scale (global, national or local) has been used to measure food availability, accessibility, and waste . Another aspect of measurement has been metric aggregation. It has been a useful way to get large-scale data, but missing data have been a problem to widespread adoption . The metrics have done a good job at predicting overall food security and at warning for upcoming potential famines. Metrics have also been implemented across scale with regional assessments providing useful data. However, the metrics have not generally explored the resiliency of the system to shocks in the production or distribution networks. The resiliency of the food system is likely to be of increasing importance as climate is projected to threaten regional production in many areas of the globe as well as many of the world’s cities . Many of these will be due to climate change . Understanding the interconnected role of risks and resilience to those risks may help understand the recovery and extent to which indicators may be used to understand both. The resilience of a system to be able to respond to perturbations is an important metric for society. Famine has a lasting effect on those whom it impacts. However, if society can recover quickly, there is the potential to better plan for how to help people under a range of different circumstances.